4.1 La Deviazione Standard.

Come si pu' osservare dalla simulazione delle varie misure del periodo di oscillazione del pendolo, i valori misurati si distribuiscono in un ampio intervallo attorno al valore della media. L'accumulo maggiore avviene attorno al valore medio ma troviamo misure, sempre piu' rare, anche a valori abbastanza lontani. Tutto cio' dipende unicamente dalle leggi del caso agenti in questo tipo di misure.

Vogliamo ora associare un valore alla precisione della misura, ovvero assegnare un errore alla misura effettuata.

Definiamo ora una nuova quantita'': la Deviazione Standard.

Data la serie di N misure $x_1, x_2, ... , x_N$ aventi come valor medio$\overline x$, si definisce Deviazione Standard e la indicheremo col simbolo$\sigma$, la seguente quantita':
 

$$\sigma^2 = \frac{(x_1 - \overline x)^2 + (x_2 - \overline x)^......ne x)^2}{N-1} = \frac{\sum^{N}_{i=1}(x_i - \overline x)^2}{N-1}$$

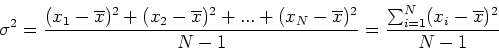
Per cui $\sigma = \sqrt{\sigma^2}$. Le deviazioni dei valori misurati dal volore medio $x_i - \overline x$ vengono definiti ``scarti''. La deviazione standard al quadrato non e' altro che la media degli scarti al quadrato.  Essa rappresenta in qualche modo la "larghezza" della distribuzione delle misure. Notiamo che al denominatore compare N-1 invece che N in quanto per poter definire media e deviazione standard occorrono almeno due misure.

Questo concetto e' esemplificato nell'animazione mostrata in figura.

Qui viene sempre simulata la misura del periodo di oscillazione del pendolo.

Premendo Start si simula una misura. Premendo il pulsante Sigma viene calcolata e visualizzata la deviazione standard insisme alla media aritmetica. La deviazione standard e' visualizzata con un segmento orizzontale da un lato e dall'altro del valore medio. Il pulsante Clear azzera l'istogramma.

Nella figura e' anche presente un cursore (d.s.) che permette di modificare il valore della deviazione standard. Premendo Clear e modificando il valore del cursore viene simulata una misura con una maggiore o minore deviazione standard. Si puo' osservare come i dati si distribuiscano in modo diverso attorno al valore medio.

Il concetto di deviazione standard e' legato al concetto di errore sulla misura effettuata.

Identifichiamo quindi come stima dell'errore commesso sul valore medio di una serie di misure il valore della deviazione standard. La misura del periodo di oscillazione del pendolo si puo' quindi esprimere nel seguente modo:
 
 

$$T = 35.5 \pm 5.4 \qquad sec$$

Dove 35.5 e' il valore medio di una certa serie di misure e 5.4 e' il valore della deviazione standard.

Aumentando o diminuendo il valore di $\sigma$ aumenta o dimuisce l'errore. Definiremo una misura piu' precisa e lo strumento utilizzato per fare tale misura piu' sensibile se l'errore su tale misura e' piu' piccolo.