Media pesata.

Da quanto osservato nei precedenti paragrafi concludioamo che il risultato di una misura di una certa quantita' x si puo' scrivere nel seguente modo:
 
  $$\overline x \pm \sigma$$

Supponiamo ora che piu' persone abbiano effettuato una misura della stessa quantita' ottenendo diversi risultati con strumenti di diversa precisione. Supponiamo di indicare con $\overline x_i$ le medie delle singole misure e con $\sigma_i$ i loro errori. Si possono combinare queste misura in un'unico risultato? E in che modo?

Ovviamente occorre utilizzare un'espressione che tenga conto della precisione della singola misura, ovvero le misure piu' precise devono contare di piu'. Quindi non faremo solo la media delle misure ma la media pesata, ovvero attribuiremo ad ogni misura un peso inversamente proporzionale all'errore di misura. Supponendo di avere N misure, la media pesata viene quindi definita come:
 
 

$$\overline x_p = \frac{\sum^{N}_{i=1}\overline x_i/\sigma^2_i}{\sum^{N}_{i=1} 1/\sigma^2_i} \qquad (3)$$

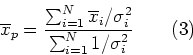
Mentre l'errore complessivo su questa media pesata viene definito come:
 
 

$$\sigma_p = \sqrt{\frac{1}{\sum^{N}_{i=1}1/\sigma^2_i}} \qquad (4)$$

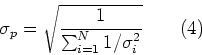
Un esempio di applicazione di queste espressioni e' mostrato in figura 7.

Notiamo, dalla (4), che nel caso in cui le varie misure abbiano tutte lo stesso errore, la media pesata coincide con la media aritmetica e l'errore sulla media sara':
 
 

$$\sigma_p = \frac{\sigma}{\sqrt{N}}$$