7.2 Legge di propagazione degli errori.

Facciamo ora una distinzione fra i vari tipi di misure possibili: misure dirette e indirette.

Chiameremo dirette quelle misure in cui uno strumento fornisce direttamente il risultato di una certa misura. Ad esempio un metro fornisce una misura diretta di una lunghezza, un orologio fornisce una misura diretta del tempo.

Chiameremo indirette quelle misure che sono ottenute mediante combinazioni algebriche di misure dirette. Ad esempio una velocita' e' ottenuta dividendo una lunghezza per un tempo.

Conoscendo ora gli errori ottenuti da misure dirette, come si propagano questi errori su quantita' ottenute mediante metodi indiretti?

Il formalismo e' molto semplice ma fa uso del concetto di derivata parziale.

Suppuniamo che sia f(x,y)una funzione di due variabili. Definiremo derivata parziale di f rispetto ad x la seguente espressione:
 
 

$$\frac{\partial f(x,y)}{\partial x}$$

Questa derivata si effettua semplicemente immaginando che la funzione f dipenda solo da x e che tutti i termini contenenti y siano assimilati a delle costanti. Analogamente se si vuola calcolare la derivata parziale rispetto ad y.

Utilizzando questo formalismo, l'errore $\sigma$ su una misura indiretta ottenuta mediante una funzione f(x,y) in cui conosciamo gli errori diretti $\sigma_x$ e$\sigma_y$ su x e y sara' data da:
 
 

$$\sigma = \sqrt{(\frac{\partial f}{\partial x})^2 \sigma_x^2 +(\frac{\partial f}{\partial y})^2 \sigma_y^2} \qquad (5)$$

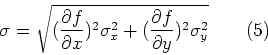
Facciamo ora alcuni esempi di applicazione della (5).

Errore sulla somma.

Supponiamo di voler calcolare l'errore sulla quantita' c ottenuta dalla somma di due quantita' a e b di cui conosciamo gli errori $\sigma_a$ e $\sigma_b$:
 
 

$$c = a + b$$

Poiche':
 
 

$$\frac{\partial c}{\partial a} = 1$$

e
 
 

$$\frac{\partial c}{\partial b} = 1$$

In questo caso otteniamo:
 
 

$$\sigma_c = \sqrt{\sigma_a^2 + \sigma_b^2}$$

mostra una simulazione di questa situazione. Nella figura sono rappresentate le Gaussiane rappresentanti le misure su a, b e il risultato su c. I cursori modificano gli errori su a e su b. Nella simulazione a e b sono posti a zero. Notiamo che nella propagazione degli errori nella somma l'errore dominante e' quallo piu' grande. In altri termini, se una quantita' a ha un errore grande, non ha alcun senso misurare b con una grande precisione, in quanto l'errore sula somma c sara' dominato da quello su a.

Errore sulla differenza:

L'errore sulla differenza e' uguale a quello sulla somma.

Infatti:

$$c = a - b$$

Poiche':
 
 

$$\frac{\partial c}{\partial a} = 1$$

e
 
 

$$\frac{\partial c}{\partial b} = -1$$

In questo caso otteniamo:
 
 

$$\sigma_c = \sqrt{\sigma_a^2 + \sigma_b^2}$$

Errore sul prodotto.

Sia:
 
 

$$c = a \times b$$

Allora:
 
 

$$\frac{\partial c}{\partial a} = b$$
 
  $$\frac{\partial c}{\partial b} = a$$

Quindi:
 
 

$$\sigma_c = \sqrt{b^2 \sigma_a^2 + a^2 \sigma_b^2}$$

Questa situazione e' simulata nella figura 10.

Prodotto di una costante per una potenza.

Supponiamo di avere un'espressione del tipo:
 
 

$$c = k \times a^n$$

Allora:
 
 

$$\frac{\partial c}{\partial a} = n a^{n-1}$$

Quindi:
 
 

$$\sigma_c = \sqrt{(k n a^{n-1})^2 \sigma_a^2} = k n a^{n-1} \sigma_a$$

Ad esempio, l'errore sull'area di un cerchio, conoscendo l'errore sul raggio e' dato da:
 
 

$$c = \pi r^2$$
 
  $$\sigma _c = 2 \pi r \sigma_r$$

Errore sul rapporto.

Sia:
 
 

$$c = \frac{a}{b}$$

Allora:
 
 

$$\frac{\partial c}{\partial a} = \frac{1}{b}$$
 
  $$\frac{\partial c}{\partial b} = \frac{a}{b^2}$$

Quindi:
 
 

$$\sigma_c = \sqrt{(\frac{1}{b})^2{\sigma_a^2} + (\frac{a}{b^2})^2 \sigma_b^2}$$

Questa situazione e' simulata nella figura 11.