Supponiamo di aver effettuato delle misure di una certa quantita' fisica che dipenda da un'altra quantita': y = f(x).
Supponiamo inoltre che, per ogni valore di x, si siano raccolti diversi
valori di y in modo tale che ad ogni misura di y sia associato un errore ![]() .
Vogliamo ora trovare la funzione f che meglio approssima i dati sperimentali.
.
Vogliamo ora trovare la funzione f che meglio approssima i dati sperimentali.
Questa procedura prende il nome di ``fit'' e la funzione f che meglio approssima i datio si chiama ``funzione di best fit''. Come facciamo a trovare questa funzione?
Uno dei metodi piu' comunemente utilizzati e' quello di definire il ![]() .
Se indichiamo con
.
Se indichiamo con ![]() ,
, ![]() e
e ![]() rispettivamente i valori della variabile indipendente i, i valori delle
quantita' misurate e gli errori corrispondenti, il
rispettivamente i valori della variabile indipendente i, i valori delle
quantita' misurate e gli errori corrispondenti, il![]() viene definito come:
viene definito come:
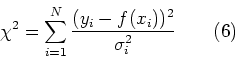
Ebbene, la funzione ![]() ,
che dipendera' da una certa serie di parametri a, b, c... sara' ottenuta
trovando il minimo della funzione di
,
che dipendera' da una certa serie di parametri a, b, c... sara' ottenuta
trovando il minimo della funzione di ![]() .
.
Il processo di minimizzare la funzione di ![]() in modo generale puo' essere alquanto complesso e va oltre lo scopo di
questo corso.
in modo generale puo' essere alquanto complesso e va oltre lo scopo di
questo corso.
Qui ci occuperemo di un caso piu' semplice: quello in cui f(x) sia semplicemente
l'equazione di una retta:
![]()
In questo caso la (6) puo' essere scritta come:
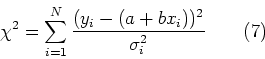
Il minimo di una funzione viene ottenuto eguagliando la sua derivata
a zero. Poiche' la funzione di ![]() dipende dai due valori incogniti a e b, chiederemo che:
dipende dai due valori incogniti a e b, chiederemo che:
![]()
e
![]()
Derivando otteniamo:
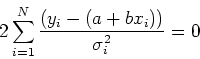
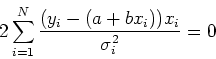
Queste due equazioni costituiscono un sistema che si puo' risolvere col metodo di Kramer.
Definiamo ora le seguenti quantita', che non sono altro che medie pesate:
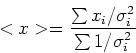
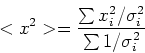
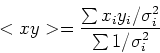
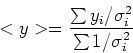
Utilizzando questi simboli i coefficienti dell'equazione della retta
saranno dati dalle equazioni:
![]()
e
![]()
Gli errori su questi coefficienti sono ottenuti nel seguente modo.
Definiamo:
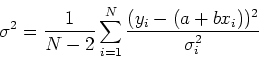
Allora:
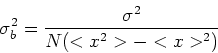
![]()