9.2 Correlazioni

Una variabile si dice che e' correlata ad un'altra se esiste una relazione matematica che le leghi, ovvero se una puo' dipendere dall'altra.

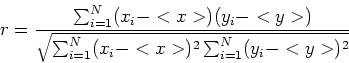
Spesso, nello studio dei fenomeni naturali, e' fondamentale stabilire se una variabile sia correlata con un'altra, in altre parole se una variabile dipende dall'altra.

La cosa non e' immediata come sembra poiche' gli errori di misura, come vedremo fra poco sono in grado, se molto grandi, di far scomparire una possibile correlazione fra due grandezze.

Data una serie di n valori di una grandezza x e una serie di n valori di una grandezza y, definiamo il ``coefficiente di correlazione'' r come:
 
 

$$r = \frac{\sum_{i=1}^{N} (x_i - <x>)(y_i - <y>)}{\sqrt{\sum_{i=1}^{N} (x_i - <x>)^2 \sum_{i=1}^{N} (y_i - <y>)^2}}$$

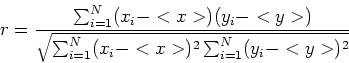
dove come prima,
 
 

$$<x> = \frac{\sum_{i=1}^{N} x_i}{N}$$

e
 
 

$$<y> = \frac{\sum_{i=1}^{N} y_i}{N}$$

Il coefficiente di correlazione e' una quantita' priva di dimensioni ed e' compreso fra -1 e +1:
 
 

$$-1 \le r \le +1$$

mostra una simulazione in cui si mostra la correlazione fra le variabili x e y. I due cursori modificano uno gli errori di misura (sigma) e l'altro la correlazione (b). Osserviamo come anche con valori di b elevati la correlazione puo' essere annullata da errori di misura molto grandi.