


Next: Prodotto vettoriale
Up: Prodotti tra vettori
Previous: Prodotti tra vettori
Il prodotto scalare tra i vettori 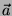 e
e 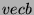 è dato da
è dato da
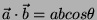 con
con 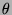 l'angolo tra i due
vettori. Dalla definizione (notate che le lettere senza freccia sopra
indicano il modulo di questi vettori) risulta che tale prodotto è uno
scalare.
l'angolo tra i due
vettori. Dalla definizione (notate che le lettere senza freccia sopra
indicano il modulo di questi vettori) risulta che tale prodotto è uno
scalare.
Proprietà : se 2 vettori sono tra loro
perpendicolari il loro prodotto scalare è
nullo.
Di conseguenza esplicitando le componenti dei vettori il prodotto
scalare sarà dato da:
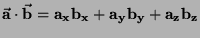 , dal momento che
valgono i seguenti prodotti scalari:
, dal momento che
valgono i seguenti prodotti scalari:
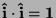 ,
,
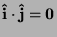 ,
,
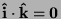 ,
,
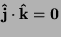 .
.
giglietto
2002-02-14