


Next: Prodotti tra vettori
Up: precorso2
Previous: Altre proprietà della somma
Un vettore è sempre scomponibile in altri vettori invertendo la
procedura della somma, ovvero vogliamo trovare due o più vettori la
cui somma fornisce il valore di partenza. Quando abbiamo questa
esigenza si cerca di scomporre il vettore dato lungo delle direzioni
note quali ad esempio gli assi cartesiani.
Definiamo come componenti di un vettore le sue proiezioni sugli
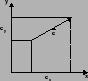
assi di riferimento. Un esempio è in fig. 8 dove sono
mostrati un vettore e le sue componenti lungo gli assi x e y.
Figure:
Scomposizione di un vettore 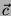 e sue componenti.
e sue componenti.
 |
In base alla scomposizione del vettore 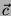 in
fig. 8 si avrà che
in
fig. 8 si avrà che
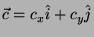 ed inoltre
ed inoltre
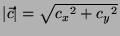 .
.
La decomposizione ci permette di maneggiare le operazioni di somma e
differenza tra vettori in modo più comodo ed evitando la procedura
grafica:
infatti se scomponiamo tutti i termini di una somma nelle componenti
lungo gli assi si avrà
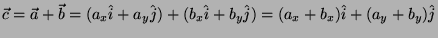 .
.
Quindi si che
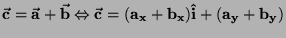 ovvero si ottiene sommando
direttamente le rispettive componenti. Analogamente per la differenza
si otterrà che
ovvero si ottiene sommando
direttamente le rispettive componenti. Analogamente per la differenza
si otterrà che
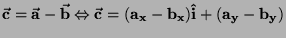 .
.



Next: Prodotti tra vettori
Up: precorso2
Previous: Altre proprietà della somma
giglietto
2002-02-14
