


Next: Somma di vettori
Up: precorso2
Previous: Equazioni dimensionali-cambiamenti di unità
Le grandezze per le quali basta un numero per rappresentarle sono dette
scalari. In molte situazioni tuttavia non basta dare un numero per
definire una grandezza. Infatti se ad esempio consideriamo lo spostamento
di un oggetto, occorre dire di quanto è spostato l'oggetto (è un numero) e
in quale direzione viene spostato. Per questo tipo di grandezze si
utilizzano i vettori: definiamo come vettore un ente individuato da
una intensitá (detta modulo), una direzione (una retta lungo la
quale agisce) ed un verso. Le grandezze vettoriali o vettori si
rappresentano con una freccia sopra (es. 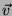 ) o per motivi
editoriali nei testi anche come v oppure v.
Il modulo di un vettore si indica esplicitamente come
) o per motivi
editoriali nei testi anche come v oppure v.
Il modulo di un vettore si indica esplicitamente come 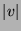 o
implicitamente se non mettiamo il simbolo del vettore (ad es. v indica il
modulo di
o
implicitamente se non mettiamo il simbolo del vettore (ad es. v indica il
modulo di 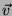 ).
Quando un vettore ha modulo unitario, ovvero quando
).
Quando un vettore ha modulo unitario, ovvero quando 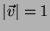 , si parla
di versori. In questo caso il simbolo usato è diverso:
, si parla
di versori. In questo caso il simbolo usato è diverso: 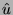 è
un versore, ovvero un vettore di area unitaria. I versori piú usati sono
quelli che indicano le direzioni degli assi cartesiani: se gli assi sono
x,y,z i loro versori sono
è
un versore, ovvero un vettore di area unitaria. I versori piú usati sono
quelli che indicano le direzioni degli assi cartesiani: se gli assi sono
x,y,z i loro versori sono 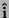 ,
, 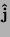 ,
, 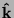 (o talvolta
(o talvolta
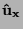 ,
,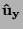 ,
,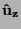 ). Ovviamente dalla
definizione risulta che per un versore si ha
). Ovviamente dalla
definizione risulta che per un versore si ha
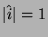 .
Proprietà dei vettori.
Prodotto di uno scalare per un vettore: è un vettore
.
Proprietà dei vettori.
Prodotto di uno scalare per un vettore: è un vettore
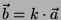 il vettore
il vettore 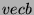 risultante ha la proprietà di
essere parallelo al vettore
risultante ha la proprietà di
essere parallelo al vettore 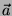 e il modulo è :
e il modulo è :
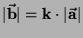 .
Quindi nel prodotto di un vettore per uno scalare il vettore
risultante è parallelo a quello di partenza ed il modulo è
moltiplicato per lo scalare.
.
Quindi nel prodotto di un vettore per uno scalare il vettore
risultante è parallelo a quello di partenza ed il modulo è
moltiplicato per lo scalare.



Next: Somma di vettori
Up: precorso2
Previous: Equazioni dimensionali-cambiamenti di unità
giglietto
2002-02-14