


Next: Differenza tra vettori
Up: precorso2
Previous: Vettori e scalari
Supponiamo di avere uno spostamento (che è un vettore) dal punto A
al punto B (vedi figura 5) e poi ancora da B a C. Lo
spostamento risultante (ovvero quello che dal punto di partenza va al
punto finale) è quello che unisce direttamente A con C.
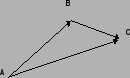
Figure 1:
Uno spostamento da A a B e poi ancora verso il punto C.
 |
Da questo esempio ne deriviamo la seguente regola generale:
se abbiamo due vettori 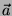 e
e 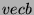 , con
, con 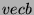 applicato
alla punta del vettore
applicato
alla punta del vettore 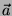 , la loro somma
, la loro somma
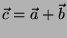 è
quel vettore
è
quel vettore 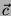 che unisce la base (il punto di partenza) di
che unisce la base (il punto di partenza) di 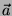 con la punta (il punto finale) del vettore
con la punta (il punto finale) del vettore
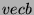 .
La stessa figura ci suggerisce una regola grafica per determinare la
somma che è detta regola del parallelogramma: ponendo i vettori
.
La stessa figura ci suggerisce una regola grafica per determinare la
somma che è detta regola del parallelogramma: ponendo i vettori
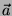 e
e 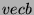 in modo da avere la stessa base, si completa la
figura costruendo un parallelogramma.
in modo da avere la stessa base, si completa la
figura costruendo un parallelogramma.
Figure 2:
Regola del parallelogramma.
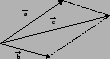 |
Il vettore somma 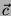 sarà
dato dalla diagonale maggiore che parte dalla comune base dei
vettori (vedi figura 5).
sarà
dato dalla diagonale maggiore che parte dalla comune base dei
vettori (vedi figura 5).



Next: Differenza tra vettori
Up: precorso2
Previous: Vettori e scalari
giglietto
2002-02-14
